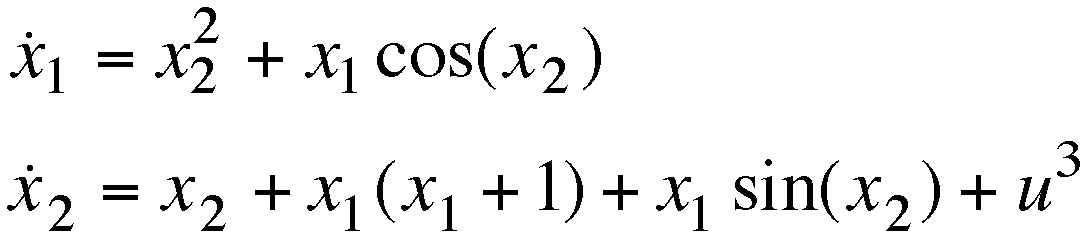
(Homeworks may be collected, and/or a quiz may be given on the due date.)
Due Friday, January 23
a) Exercises 2.1, 2.2, 2.6, 2.10
b) Computer Exercise 2.1
c) Linearize the following system about x=0, u=0.
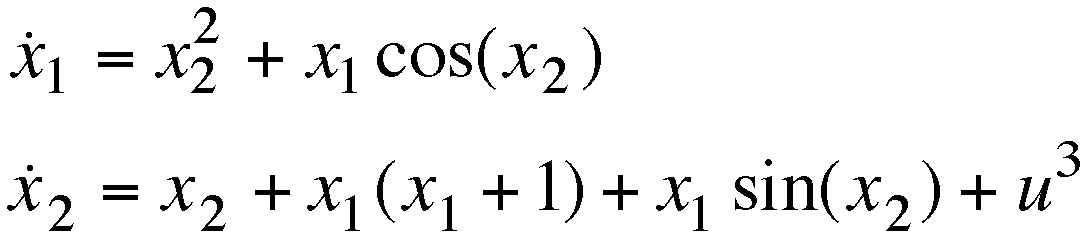
Due Friday February 6
a) SVD related problems from Hmk #1
b) Exercises 2.5, 2.13, 2.14, 2.15
c) Computer Exercise 2.2
Due Friday February 20
a) Exercises 2.15, 3.1, 3.3, 3.4
b) Write MATLAB program to do pole positioning using method described in class
c) Computer Exercise 2.3 (use program developed in b)
Due Friday February 27
This Homework will not be collected. Exam #1 will be given on this date.
Due Friday, March 13
1) Exercises 3.2, 3.7, 3.11, 3.12
2) Computer Exercise 3.1
Due Friday, April 3
Consider the following model of a frictionless dc motor:
where the states are motor position and velocity. Suppose we want to control the position of the motor
![]()
and our performance index is
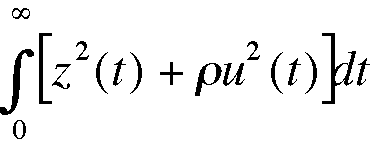
(a) Determine the steady state solution of
the Riccati Equation.
(b) Determine the steady state optimal control law.
(c) Compute the closed loop poles. Sketch the loci of the closed loop
poles as r (rho) varies.
(d) Using the following numerical values, simulate and plot the response
of the closed loop system to the initial state x(0) = [0.1 rad 0 rad/s]'.
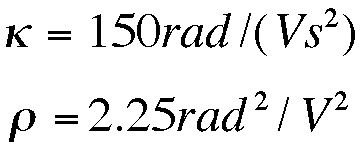
Due Friday, April 17
1)
Exercise 6.5 from text.
2) Computer Exercise 6.1 from text.
3) Consider the following position control system, where the first
state is postion and the second state is velocity.
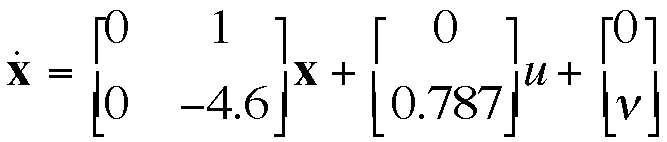
where n is a random disturbance torque satisfying
![]()
where w is white noise with intensity 50. The performance index is
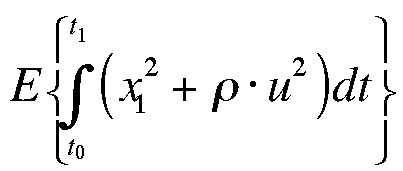
(a) Find the steady state optimal stochastic
controller.
(b) Find the steady state rms values of position error and input.
4) Exercises 7.5, 7.7, 7.8, 7.9
This homework will not be collected. Exam #2 will be given on the due date.